[This page is a draft. Please help me improve it by sending me comments.]

What is Understanding?

In Natural Language Processing (NLP), a branch of Artificial Intelligence (AI), one of the main goals is to create computer systems that can understand human languages such as English, Russian, and Japanese.

But what does it actually mean to understanding human languages? When can we say that a computer really understands a Natural Language (NL) text or speech input? For that matter, how can we even be sure that a fellow human really understands something we say or write?

The question of understanding is, of course, a complex philosophical, psychological, and linguistic issue. Yet one practical way to address it is to ask our fellow human or computer a series of questions about the NL information we told them, and see if they can answer these questions correctly. We have all experienced, in our childhood, this kind of method: we were given reading comprehension tests in school, such as this one:

John was hungry. He wanted to eat the apple he brought in his bag. He searched for the apple in the bag, but couldn't find it.

1. Did John eat the apple?
2. Did John lose the apple?
3. Why did John want to eat the apple?
4. What couldn't John find?
5. How did John feel after searching for the apple?

Children are given such stories, followed by a comprehensive set of questions, which ask about many different aspects related to the story. If the reader answers all these questions correctly, we can say with some confidence that the reader indeed understands the text.

NLP and Understanding

While full Natural Language Understanding is the “holy grail” of NLP, it is also far beyond the state-of-the-art (in fact, some say it is “AI-complete“). Most existing NLP systems, despite their usefulness and benefits, cannot be said to really understand the texts they are processing.

For instance, a textual search engine (as in google.com) doesn’t really understand texts, it only matches the search query words to the words in the texts, with a few morphological variations (search for “baby” and get a text containing the plural form “babies”) and possibly some synonyms (search for “notebook” and get a text containing the word “laptop”). It cannot answer the sort of reading comprehension questions shown above.

Similarly, automatic translation systems (such as translate.google.com) contain useful knowledge about the connection between phrases in different languages, but they are not designed to answer reading comprehension questions. In fact, even for the translation task itself, there are some cases that expose the lack of real understanding of these systems, as the following example demonstrates.

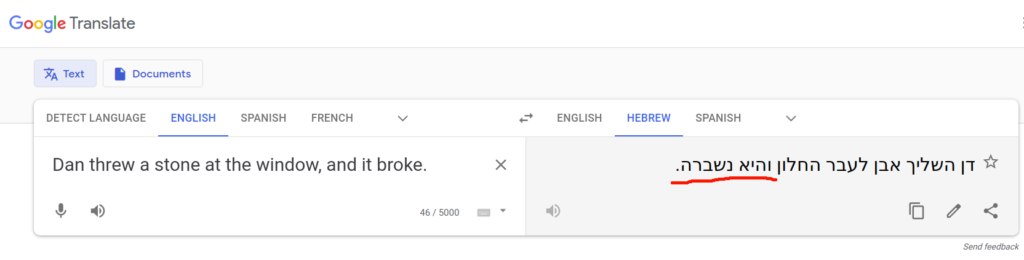
The screenshot below shows the input on the left – the English text “Dan threw a stone at the window, and it broke”. Humans possess knowledge about the physical world, specifically that stones are hard, windows are made of thin sheets of glass which are fragile, and propelling a hard object at a fragile object usually causes the latter to break. This allows a human reader to quickly understand that it was the window which broke, and not the stone, so “it” refers to “the window”. A computer translating from English to Hebrew must possess this knowledge to produce a correct translation, because in Hebrew, nouns have gender (masculine and feminine), and the noun “stone” is feminine while the noun “window” is masculine. A correct translation is “Dan zarak even al hakhalon, vehu nishbar” (in the masculine) rather than “Dan zarak even al hahklon, vehi nishbera” (in the feminine). The google translator lacks such knowledge about the physical world, and thus outputs a wrong translation:

There has been some progress in recent years towards creating Question Answering systems. Such systems do in fact try to incorporate at least some world knowledge and linguistic knowledge about a particular domain, or use some other techniques which attempt to find pieces of information in texts which may be relevant to the user’s question even if not directly answer it. However, they mostly focus on basic factual statements and questions such as “Who is the president of the United States?”. Moreover, they usually do not correctly produce conclusions that can only be inferred from combining different pieces of information that appear throughout the text. Even simple stories such as the one about John and his apple above cannot yet be understood correctly.

What is needed for Natural Language Understanding?

Creating a computer system that can genuinely understand even simple texts as above is a huge challenge. This is because NL texts can talk about almost any topic. To correctly understand them, the computer needs to have knowledge of several kinds, including at least:

• General knowledge about the world
• Linguistic knowledge about the text’s language

The scope of the first kind of knowledge (aka “Commonsense Knowledge“) is practically unbounded, as the text may talk about almost anything: all kinds of objects, their composition and interrelationships, properties such as colors and textures, space and time, human emotions, motivations, thoughts and desires. Understanding a text may require knowledge of cause and effect and “everyday physics” (e.g. what happens when you drop a glass full of water on the floor), and much much more. This knowledge is not specified explicitly in the text, because the author assumes that the human reader already has this knowledge. The reader can use her commonsense reasoning abilities to combine that general knowledge with the information explicitly given in the text to infer the required conclusions from it.

The second kind of knowledge, linguistic knowledge, is also very extensive. Part of it is a lexicon: a mapping from words and expressions in the language to their meanings, which are pieces of knowledge about the world. For example, the noun “bank” has (at least) two meanings, one is the financial institution, the other is the side of a river. Meanings may be complex, especially for verbs. If “John succeeded to open the door” that implies he in fact opened the door, and also that he first tried to open the door (which posed at least a minor challenge). But if “John refused to open the door”, that implies he did not open the door (at least initially), and that someone else previously asked or demanded him to do so.

Structural Semantics

So general world knowledge is virtually unbounded, and lexical knowledge is extremely extensive. Research on these directions is interesting and important, and will undoubtedly continue for a very long time. But here, I would like to direct our attention to another kind of necessary knowledge which, unlike the previous two, is reasonably bounded. While it’s not trivial, there is good hope that we can correctly capture it quite comprehensively and make good use of it. More importantly – for our goal of advancing understanding of NL texts, this knowledge will allow us to create systems that can do some logical inferences from NL texts and answer logical questions about them, thus demonstrating at least some level of understanding. I’m referring here to the linguistic knowledge about Structural Semantics.

Structural Semantics (aka “Formal Semantics” or “Compositional Semantics”) is the branch of linguistics that studies the structural meaning of natural language sentences, in a somewhat analogous way to the semantics of formal languages such as logical languages and programming languages.

Reminder: Semantics of a Formal Language

To understand what this idea means, let us first recall what semantics means in the context of formal languages. There are several different approaches (see: Semantics of Logic and Semantics in Computer Science), but here we’ll mention the approach that is usually used for linguistics semantics. As an analogy, let’s take as an example the language of First-Order Logic (FOL), and the kind of semantics usually presented for it (“Tarskian Semantics“). The following assumes you have basic familiarity with FOL; if you don’t, I suggest you search online for an introductory text or class. I briefly recite here part of the definition of FOL, to help us see the similarity to Structural Semantics, but you may quickly skim through it.

The language of FOL has logical symbols and non-logical symbols. The logical symbols include the logical connectives ¬ (“not”), ∧ (“and”), ∨ (“or”) and → (“implies”), as well as the quantifiers ∀ (“forall”) and ∃ (“exists”). The non-logical symbols include constants (representing individual objects), function symbols, and predicate symbols (representing relations over individuals). Logical symbols have a fixed meaning, while the meanings of non-logical symbols depend on the domain (more on that below).

The syntax of FOL specifies how expressions are formed. That are two types of expressions: terms and formulas. Terms, which intuitively represent objects, include variable symbols, constant symbols, and function symbols applied on terms (e.g.: “f(x,c,h(d))“). Formulas, which intuitively represent true or false statements about objects and relations, are defined recursively. An atomic formula is a predicate symbol applied on terms (e.g.: “R(c,f(x,d))“). If A and B are formulas, and v is a variable symbol (such as x or y) then the following are also formulas: (¬A), (A∧B), (A∨B), (A→B), ∀v.[A], ∃v.[A] (parentheses may be omitted if there is no confusion). So an example of a complex formula is: ∀x.[(P(x)∧L(x,h(x))) → ∃y.[S(x,y)∧L(x,y)]] .

The semantics of FOL specifies what expressions in the FOL language mean. Logical symbols (such as ∧ and ∀) have a fixed meaning, but the meaning of non-logical symbols depend on an interpretation in a specific model. A model M consists of a domain, which is a non-empty set D of individuals, and an interpretation function Intr that assigns a denotation (“meaning”) to each non-logical symbol: For a constant symbol such as c, its interpretation is some individual in D (i.e. Intr(c)∊D); for a n-ary function symbol, its denotation is some function from Dⁿ to D; and for an n-ary predicate symbol, its denotation is some subset of Dⁿ. The interpretation of more complex terms and formulas is given recursively, where each syntax rule has a corresponding semantic rule. For example, take the syntax rule which says: if A and B are formulas then A∧B is a formula. Its corresponding semantic rule says: the interpretation of A∧B (according to Intr and a variable assignment g) is the value true if the interpretations of both A and B (under Intr and g) are true; otherwise the interpretation of A∧B is false.

Of course, the full definition covers all syntax and semantic rules. The main point to notice here is that the definition of the semantics of FOL has two parts: one part which is fixed – the meaning of the logical symbols and the semantic interpretation rules, and another part which depends on particular models and interpretations of the non-logical symbols. Also, the semantic rules follow the Principle of Compositionality: The meaning of a complex expression is determine by the meaning of its parts and the manner in which they are combined (i.e. the syntax rules).

Structural Semantics in Linguistics

In an analogous manner to the semantics of a formal language mentioned above, Structural Semantics (of natural languages) focuses on the structural meaning of sentences, i.e. the logical literal meaning of sentences after abstracting away the specific lexical meanings of non-function words.

Just like the logical symbols in FOL, we have functional expressions (aka “Function Words“) in NL. These are the “operators” of the language, and they have a fixed meaning which (by and large) does not depend on the context. Natural languages have a much richer set of such operators compared to FOL. Here are a few examples:

• Logical operators: and, or, not, if, then, unless, only, except, but, however, …
• Quantifiers: every, some, no, any, most, few, …
• Numeric quantifiers: at least N, at most N, more than N, no more than N, …
• Modal operators: must, may, can, cannot, possibly, necessarily, …
• Referring terms: the, a, he, she, they, his, her, hers, this, that, …
• Auxiliary verbs: be, is, are, was, been, do, did, have, has, become, …
• Temporal/spacial relations: before, after, at, on, inside, above, below, adjacent, …
• Intensifiers: very, almost, somewhat, especially, …
• Cardinal and ordinal numbers: one, two, …, thirty, …, first, second, …, tenth, …
• Question words: what, who, whom, when, where, which, why, how, …

Now, what is the analog in NL of the non-logical symbols of FOL? Well, natural language has content words such as nouns, verbs, adjectives, and adverbs. But there is a difference. Non-logical symbols in FOL can get any possible interpretation, depending on the model chosen (e.g. a unary predicate symbol P can be interpreted as any subset of the domain D of individuals, depending on the domain and interpretation Intr). In contrast, each content word in a particular language (such as English) has only a small number of possible meanings (e.g. “notebook” can mean a paper booklet or a laptop, but cannot have arbitrary meanings).

The meanings and usage of these content words are studied in the linguistic field of Lexical Semantics. But Structural Semantics itself does not care about these lexical meanings. It only cares about the meanings of functional words, the morphology and syntax of the language, and the semantic composition rules.

Logical Meaning and Inference

We saw that Structural Semantics ignores lexical meanings of content words. But then – what are we left with? Well, what remains is exactly the logical (literal) meaning of sentences, as determined by the meaning of functional words and syntax. This logical meaning allows us to focus on the kinds of logical inferences we can do in natural language.

To illustrate this point, let’s invent a few words, to emphasize that we don’t care about their lexical meanings. Let’s have a noun “pencheon”, an adjective “sopomous”, and a proper name “Jorrdek”. Now, regardless of what these actually mean, we can still say that the following inference (syllogism) is logically valid:

Assumptions:
* All pencheons are sopomous.
* Jorrdek is a pencheon.
Conclusion:
Jorrdek is sopomous.

Even without knowing anything about the lexical meanings of the invented words, we can safely say that the conclusion indeed can be logically inferred from the structure of assumptions. The only required knowledge to support this inference includes:

• Basic linguistic knowledge about morphology (“pencheons” is the plural form of “pencheon”) and syntax (e.g. “All pencheons” is the subject of the sentence)
• The meaning of the functional terms “all”, “are”, “is”, and “a”
• Semantic rules which specify how the meanings of the functional terms interact with the text’s morphological and syntactic analysis to produce the structural meaning of the entire text.

This structural meaning could then be represented using some expression in a mathematical Meaning Representation Language (MRL). This formal language has well-defined semantics. So unlike Natural Language, we know exactly what each operator and expression in this formal language means. For instance, to continue the example above, if we choose First-Order Logic (FOL) as our MRL, then the above text is translated to these FOL statements:

Assumptions:
* ∀x. [Pencheon(x) → Sopomous(x)]
* Pencheon(jorrdek)
Conclusion:
Sopomous(jorrdek)

Now we can easily see that the conclusion indeed logically follows from the assumptions, even if we don’t know the interpretation of Pencheon, Sopomous, and jorrdek. (We only know that the first two are predicates, and the last one is a constant referring to some individual object in the domain of objects).

The upshot is that Structural Semantics allows us to translate NL texts to well-defined meaning representations that expose the logical inferences we can do based on the information in the text.

More Information

So what are the actual details of Structural Semantics for English and other languages? What are the defined meanings of the functional expressions? What are the semantic rules? There is a LOT to say about that, and I will dedicate many more posts to answer these and related questions (I will post here links once these posts are ready).

What is beyond Structural Semantics?

Before we continue, I want to make sure we are clear about what Structural Semantics includes and does not include. I re-emphasize that it only encompasses the literal meaning of sentences, abstracted from specific concepts of non-functional terms. I wrote a separate post that surveys some types of meaning that are not included in this body of knowledge. You can read it here at a later time.

Why is Structural Semantics important for NLU?

Now that we know what Structural Semantics is, and what it does not included, the question is – what is it good for? How useful is it for NLU applications? In particular, how can it help us create systems that can answer questions about a given text, thus demonstrating at least some level of understanding? There are many applications that would benefit from this kind of knowledge, and I dedicated another post to survey them.

What’s the Next Step?

If your curiosity got piqued about Structural Semantics, and you got convinced (after reading my other post) that it’s an interesting topic and is useful for advancing the state-of-the-art in NLU, you might wonder: what’s the next step?

The next step is to learn more about Structural Semantics, do research to extend its current scope, and use it in NLU applications. To that end, I am doing a research projects called PULC: Precise Understanding of Language by Computers. Specifically, I am working on creating a computer system that can understand logic puzzle texts and solve them correctly. I invite you to read about it here: Automatic Understanding of Natural Language Logic Puzzles.